DIBUJO TÉCNICO
GEOMETRÍA PLANA
Mediatriz. bisectriz, polígonos, curvas, espirales, tangencias.
sistema diédrico, vistas.
TANGENCIA Y ENLACES
http://www.educacionplastica.net/tangen.htm
http://www.slideshare.net/qvrrafa/tema-5-tangencias-y-enlaces-presentation
La homología es una transformación homográfica que cumple las siguientes leyes:
- Dos puntos homólogos están alineados con un punto fijo llamado centro de homología. -
- Dos rectas homólogas se cortan siempre en una recta fija llamada eje de homología.
La homología solo mantiene el número de lados de la figura inicial, las demás características no se conservan: los ángulos, paralelismos, perpendicularidades, distancias, proporciones, etc. se verán alterados.
ELEMENTOS EN UNA HOMOLOGÍA:
Así la intercambiabilidad de los elementos de las maquinas y la especialización de las industrias provoco el que se necesitasen unas normas que rigiesen en un principio las medidas y más tarde los procesos.
Originarias de Alemania, las normas DIN fueron las primeras que se escribieron. Más tarde cada país impuso sus normas, en la mayoría de los casos simples copias de las alemanas.Con el aumento del comercio internacional se comprendió que era preciso una normativa internacional y de ahí el nacimiento de las normas ISO, aceptadas por la mayoría de los países.
ejercicios escala
http://trazoide.com/escalas.html
2º-SISTEMAS DE PROYECCIÓN:SISTEMA EUROPEO.SISTEMA DIÉDRICO
Consultar apuntes
- VISUALIZACIÓN Y EJERCICIOS DE VISTAS, CON PROGRAMA INTERACTIVO.MUY INTERESANTE PARA Y TRABAJAR EN CLASE
+18.06.06.png)
4º-SISTEMA DIÉDRICO DE PROYECCIÓN. CONCEPTOS BÁSICOS
GEOMETRÍA PLANA
VIDEOS
TRAZADOS BÁSICOS:
ESCUADRA Y CARTABÓN: PARALELAS Y PERPENDICULARES, MEDIATRIZ Y BISECTRIZ Y TEOREMA DE THALES
http://ntic.educacion.es/w3//eos/MaterialesEducativos/mem2001/dibujotecnico/Construcciones%20de%20dibujo%20tecnico/msp_cb.htm
TRAZADO VIDEO DE E MEDIATRIZ
TRAZADOS BÁSICOS:
ESCUADRA Y CARTABÓN: PARALELAS Y PERPENDICULARES, MEDIATRIZ Y BISECTRIZ Y TEOREMA DE THALES
http://ntic.educacion.es/w3//eos/MaterialesEducativos/mem2001/dibujotecnico/Construcciones%20de%20dibujo%20tecnico/msp_cb.htm
TRAZADO VIDEO DE E MEDIATRIZ
VIDEO SOBRE LA DIVISIÓN DE UN SEGMENTO EN PARTES IGUALES, (TEOREMA DE THALES)
http://www.youtube.com/watch?v=uGWRX-4GyJs&feature=related
http://www.youtube.com/watch?v=uGWRX-4GyJs&feature=related
Recta o curva tangente a otra, es aquella que la toca sin cortarla. En este apartado se trata de reconocer y construir elementos tangentes partiendo de unos datos establecidos.
El concepto de tangencia es de suma importancia para la resolución de enlaces, ya que, para la construcción de un enlace, será necesario contar con los puntos de tangencia.
Para trazar líneas tangentes (rectas o curvas), primeramente será necesario determinar cuales son los puntos de tangencia.
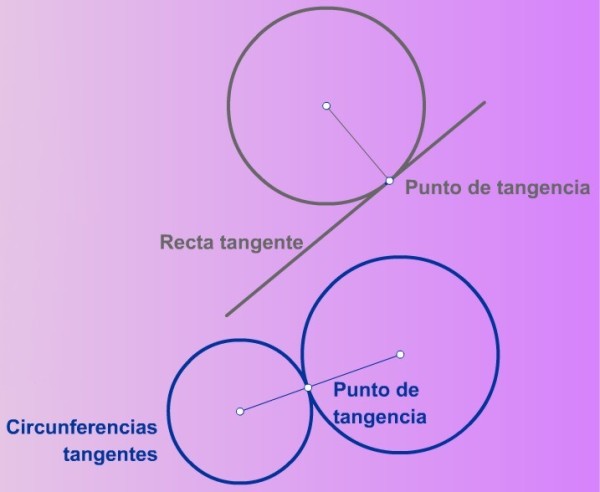
Características generales.Se llama recta tangente, a la recta que toca a una circunferencia (o arco de circunferencia) en un único punto, llamado punto de tangencia.
El radio de la circunferencia, correspondiente al punto de tangencia, es perpendicular a la recta tangente.
Análogamente, dos circunferencias son tangentes si se tocan en un único punto. El punto de tangencia se situa en la línea que une los centros de las dos circunferencias.
EJERCICIOS REALIZADOS DE TANGENCIAS
http://www.educacionplastica.net/tangen.htm
http://www.slideshare.net/qvrrafa/tema-5-tangencias-y-enlaces-presentation
ENLACES
Enlace y tangencia son términos estrechamente relacionados. A través del enlace deberemos unir dos líneas (ya sean rectas o curvas) de tal forma que esta unión sea armónica. Para ello es necesario contar con los puntos de tangencia.
Características generales.
Enlace es la unión armónica de dos líneas, ya sean curvas o rectas, de modo que parezcan una línea continua.
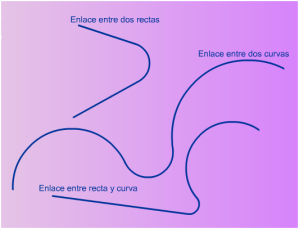
Tipos de enlace:
- Entre dos rectas
- Entre dos curvas
- Entre recta y curva
Tipos de enlaces
Para trazar enlaces de cualquier tipo, se ha de seguir siempre las mismas operaciones.
OPERACIONES GENERALES:
- Hallar el centro de enlace. Es la primera operación para hallar el punto desde donde se va a realizar el enlace.
- Se hallan los puntos de tangencia. Los puntos de tangencia son los datos necesarios para saber donde empieza y donde acaba el enlace.
- Se traza el arco del enlace. Se traza el arco repasando todo el enlace y se remarcan las líneas enlazadas.
- -IGUALDAD,SEMEJANZA, EQUIVALENCIA, GIRO, HOMOTECIA
HOMOTECIA
La HOMOTECIA es una transformación geométrica en el plano en la que, dado elcentro de homotecia O y una razón de homotecia K≠0 que puede ser positiva + onegativa -, a todo punto A le corresponde otro punto A´, alineado con el centro de homotecia O, cumpliéndose que OA´/OA= k.
Se trata de una transformación ISOMÓRFICA dado que la figura que obtenemos tras su aplicación tiene la misma forma, aunque no necesariamente el mismo tamaño. La transformación puede ser así mismo DIRECTA (se conserva el sentido del plano), siVK>0 o INVERSA (la figura homotética no conserva el sentido del plano de la original), si K<0 b="">.
Se trata de una transformación ISOMÓRFICA dado que la figura que obtenemos tras su aplicación tiene la misma forma, aunque no necesariamente el mismo tamaño. La transformación puede ser así mismo DIRECTA (se conserva el sentido del plano), siVK>0 o INVERSA (la figura homotética no conserva el sentido del plano de la original), si K<0 b="">.
- Si los puntos A y A´están al mismo lado de O la homotecia es directa o positiva
- Si los puntos A y A´están a ambos lados de O la homotecia es inversa o negativa
- Si K=1 y el centro de Homotecia es propio, tenemos una identidad, donde A=A´.
- Si K=-1 la homotecia se transforma en una simetría central (o un giro de 180º)
- EJERCICIOS/VIDEOS
HOMOLOGÍA
- Dos puntos homólogos están alineados con un punto fijo llamado centro de homología. -
- Dos rectas homólogas se cortan siempre en una recta fija llamada eje de homología.
La homología solo mantiene el número de lados de la figura inicial, las demás características no se conservan: los ángulos, paralelismos, perpendicularidades, distancias, proporciones, etc. se verán alterados.
Dos figuras planas son homográficas cuando se corresponden punto a punto y recta a recta de modo que a cada punto y recta de una figura le corresponden un punto y una recta de la otra. Dos secciones de una misma radiación son homológicas si se cumple que:
- Los puntos homólogos están alineados con uno llamado centro de homología.
- Rectas homólogas se cortan en puntos de una recta llamada eje de homología.
Tipos de homología
Existen 2 tipos de Homología:
- Homología directa: se da cuando un punto y su homólogo se encuentran en diferentes lados del Eje.
- Homología inversa: se da cuando un punto y su homólogo se encuentran al mismo lado del Eje.
Determinación de una homología
Una homología queda determinada dando:
A) El centro, el eje y un par de puntos homólogos
B) El centro, el eje y un par de rectas homólogas
C) Tres puntos no alineados y sus homólogos. Los puntos homólogos estarán alineados con el centro de homología y las rectas homólogas que los unen se cortarán en el eje de homología.ELEMENTOS EN UNA HOMOLOGÍA:
CENTRO DE HOMOLOGÍA: Es el foco de la radiación de rectas que pasan por pares de
puntos homólogos. Es el punto donde se cortan todas las rectas que unen un punto con su homólogo en una homología.
EJE (O): Es el lugar geométrico de los puntos que son homólogos de sí
mismos (puntos dobles).
Rectas homólogas siempre convergen en el eje.
puntos homólogos. Es el punto donde se cortan todas las rectas que unen un punto con su homólogo en una homología.
EJE (O): Es el lugar geométrico de los puntos que son homólogos de sí
mismos (puntos dobles).
Rectas homólogas siempre convergen en el eje.
(centro de O homología)
RECTAS LÍMITE: Es el lugar geométrico de los puntos cuyos homólogos están en el infinito. Es una recta formada por puntos que no tienen homólogos (puntos impropios). Son dos RL1 y RL2 , también llamadas RL y RL´
Una homología queda determinada conociendo los siguientes datos:
Una homología queda determinada conociendo los siguientes datos:
1- El eje, el centro y un par de puntos homólogos.
2- El centro y dos pares de rectas homólogas
3- Un punto doble y dos pares de puntos homólogos. 4- El centro, el eje y el coeficiente de homología
5- El centro y las dos rectas límite.
6- El centro, una recta límite y dos puntos homólogos. 7- El centro, el eje y una recta límite.
8- Dos figuras homólogas.
2- El centro y dos pares de rectas homólogas
3- Un punto doble y dos pares de puntos homólogos. 4- El centro, el eje y el coeficiente de homología
5- El centro y las dos rectas límite.
6- El centro, una recta límite y dos puntos homólogos. 7- El centro, el eje y una recta límite.
8- Dos figuras homólogas.
-NORMALIZACIÓN
Así la intercambiabilidad de los elementos de las maquinas y la especialización de las industrias provoco el que se necesitasen unas normas que rigiesen en un principio las medidas y más tarde los procesos.
Originarias de Alemania, las normas DIN fueron las primeras que se escribieron. Más tarde cada país impuso sus normas, en la mayoría de los casos simples copias de las alemanas.Con el aumento del comercio internacional se comprendió que era preciso una normativa internacional y de ahí el nacimiento de las normas ISO, aceptadas por la mayoría de los países.
El dibujo normalizado se divide en varias partes :
- Vistas - Es la forma de representar un objeto desde varios puntos de vista ortogonales. Habitualmente se utilizan tres vistas, alzado, planta y perfil. Existen dos sistemas principales, el sistema del primer diedro (europeo) y el del tercer diedro (americano).
- Cortes - Son las vistas de una pieza a la que se le ha realizado un corte imaginario para que sea más visible la parte interior.
- Despieces y conjuntos - Muestran los distintos elementos que forman una maquina o parte de ella, indicando la colocación o posición de cada una.
- Acotación - Para la fabricación de una pieza es necesario indicar las dimensiones de esta. Estas medidas forman la acotación que se asan en una serie de convenios o normas para que sean entendibles por todos.
- Escalas - La imposibilidad, por tamaño excesivo o minúsculo, de representar un objeto a su tamaño natural provoca el que se deba aumentar o reducir su tamaño, es decir, aplicar una escala.
- Normas - Recomendaciones sobre representacioes y sus soportes, como tamaños de papel (formatos), su plegado y los cajetines.
- http://trazoide.com/introduccion-2.html
- http://trazoide.com/videos/normalizacion/
- ESCALA
- VIDEO CONSTRUCCIÓN ESCALA
- http://trazoide.com/videos/escala-grafica/
PROGRAMA INTERACTIVO PARA EJERCICIOS DE DIÉDRICO, desde vistas hasta recta y plano.
VISTAS
OTRO PROGRAMA
3º-SISTEMA AXONOMÉTRICO.PERSPECTIVA CÓNICA
4º-SISTEMA DIÉDRICO DE PROYECCIÓN. CONCEPTOS BÁSICOS
A-)-REPRESENTACIÓN DEL PUNTO
B-)- REPRESENTACIÓN DE LA RECTA
C-)- REPRESENTACIÓN DEL PLANO
D-) OBTENER TRAZAS DE UN PLANO
1º-Obtención de un plano , dados tres puntos no alineados
2º-Obtención de un plano por dos rectas que se cortan
3º-Obtención de un plano por un punto y una recta
E-) RECTA DE MÁXIMA PENDIENTE Y RECTA DE MÁXIMA INCLINACIÓN
F-) PERTENENCIA
G-) PARALELISMO ENTRE RECTAS.PARALELISMO ENTRE PLANOS
G-) INTERSECCIÓN ENTRE PLANOS
INTERSECCIÓN ENTRE PLANOS CUYAS TRAZAS SE CORTAN FUERA DEL DIBUJO
No hay comentarios:
Publicar un comentario